演算法,應該是現在學 CS 最潮、最常被提到的詞,
那演算法到底是什麼呢?
用白話文說起來,就是指『設定一套解決一個問題的固定流程』。
而這個流程會用一些數學符號表示,並再用程式實作出來,
所以一個好的演算法跟一個壞的演算法比起來,
能用更有效率、更少資源來解決一個相同的問題。
例如迴圈的概念其實就是一個最基本、原始的演算法,
使用更少的程式碼,去做同一件運算。
也能參考維基百科上的演算法流程圖,說明解決電燈沒電的問題:
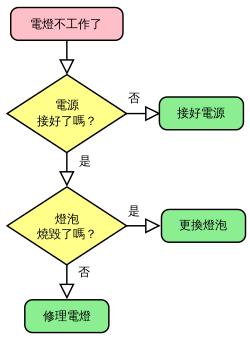
這樣應該有對演算法的概念更了解了吧~~?
那我們就要先來說明演算法的核心該有哪些項目:
一個完整的演算法,至少要包括上述的要素。
演算法的類別可以簡單分成幾項常見的設計模式,
為了讓讀者能更清晰了解模式的差別,我們先設定一個假定的問題,
Q - 台灣勞工的平均年收入多少? (傷心)
簡單可以拆成兩種,完全遍歷法和不完全遍歷法:
完全遍歷法: 把每個有可能被運算的元素都運算過一次。
—> 追殺每個台灣有在賺錢的人,把他所有賺錢的紀錄給榨出來
不完全遍歷法: 因為資源上的限制或實作上的困難性,只針對部分元素運算。
—> 追殺看得順眼,台灣有在賺錢的人,把他所有賺錢的紀錄給榨出來
而不完全遍歷法又可分為下列幾項:
分治法
定義: 把一個問題拆成許多個小問題,並把這些問題的答案聚集起來能當作大問題的解答
—> 先收集台灣不同縣市的平均年收入,再做加總平均計算
動態規劃法
定義: 分治法的延伸,當分割出來的小小問題一直出現,則儲存起此問題的答案,避免重複運算一樣的問題。
—> 在收集縣市內每個人的收入時,假定會透過姓氏去跑一個會運算10秒鐘的公式( 例如,姓劉要課4.234% ,姓李要課 6.32423%,數字是運算結果 ),那就直接儲存這些結果在某變數中,下次需要計算時直接取用那個變數即可。
貪婪演算法
定義:如果最終的演算,是透過好幾個有序列性的運算取得,則每次運算只取最佳解做下次運算。
—> 我可以先透過『訪談本人』或『訪談國稅局官員』拿到原始資料後,再針對原始資料,做相關聯資料的歷史資料剖析。雖然『訪談國稅局官員』拿到的資料,經過歷史剖析後不一定是最正確的,但是『訪談國稅局官員』可以拿到的資料是當下最佳的,所以我先選用這個方法。
複雜度,可以說是評估演算法品質的重要指標,
而且複雜度的顯示機制,可以讓評估者快速比較差異過大的兩個演算法效益。
而這個指標,又分成『時間複雜度』和『空間複雜度』兩種。
時間複雜度是最重要的指標,
因為他是指,完成這個演算法,可能需要耗費的時間。
一般的寫法會像 『 O(1) 』,唸作『 Big O, 1 』。
而 O(1) 的意思,指的是,會執行 1 次的運算。
例如:
a = 5 + 1
再來,要來很酷的喔!
O(n),唸作『 Big O, n 』
指的是以下的演算法:
for i in range(n):
a = 1 + i
這個程式,會執行『 n 』次,
因此這個演算法會根據 n 的大小去變動。
再來,是這個: O(n^2),也就是 n 的平方。
for i in range( 5 ):
for j in range ( 3 ):
a = 1 + j
這個程式是一個很經典的『雙重迴圈』,
第一個迴圈會把『第二個迴圈』執行五次,
而第二個迴圈,會把『 a = 1 + j 』 執行三次,
所以『 a = 1 + j』 這個主程式共被執行了 5 * 3,也就是 15 次。
如果用 n 來表示呢?
for i in range ( n ):
for j in range( n ):
a = 1 + j
這個迴圈就會執行 n * n,也就是 n 的平方次,
所以他的時間複雜度就是 O( n^2 )。
因此我們會透過判斷這些時間複雜度內 n 的狀況,
評估演算法的效率。
像是當 n = 3 時,可能沒有太大的差距,
但當 n = 1000 時,兩個演算法的效率就會非常巨大。
這樣各位讀者對時間複雜度的判斷有更有概念了嗎?
空間複雜度的概念,其實相對時間複雜度簡單許多,
他指的是這段程式對於『記憶體的消耗程度』。
有些程式會宣告過多的變數,或是建立過多的物件,
因此造成記憶體過度使用,
但以目前的趨勢來說,一般的網路應用,
空間複雜度不太會是主要評估的部分。
如果有任何問題,或是指證文中的錯誤,歡迎寄信給我或留言在下面喔~
